TP3 Collisions hash et limites de RSA

L’objectif de ce TP est d’apprécier quelques attaques sur les fonctions de hachage et les implémentations de RSA.

Calcul de hash

Quand on visite par exemple les distributions d’Alpine Linux, on peut télécharger :

• l’image binaire alpine-standard-3.19.1-x86_64.iso (lien direct) ;
• un fichier alpine-standard-3.19.1-x86_64.iso.sha256 (lien direct).

Le deuxième fichier .sha256 est le résultat d’une fonction de hachage cryptographique.

En ligne de commande

Question 1.1 que permet de vérifier le fichier à l’extension .sha256 ?

Question 1.2 (bonus) donner la commande utilisant sha256sum pour faire la vérification précédente.

Question 1.3 (bonus) donner la commande utilisant openssl pour faire la même vérification.

En Python

La bibliothèque standard Python comporte les modules hashlib et hmac. On reprend ci-dessous un exemple de calcul du hash d’un fichier.

import hashlib

def get_sha256_hashlib(filename, buffer_size=2**13):
    """See https://www.pythonmorsels.com/reading-binary-files-in-python/"""
    file_hash = hashlib.sha256()
    with open(filename, mode="rb") as file:
        while chunk := file.read(buffer_size):
            file_hash.update(chunk)
    return file_hash.hexdigest()

Question 1.4 compléter le script précédent pour vérifier l’image binaire, c’est-à-dire, faire en Python ce qui a été fait précédemment en ligne de commande.

Question (bonus) 1.5 implémenter une fonction get_sha256_cryptodome() qui fait la même chose que get_sha256_hashlib() mais utilisant Crypto.Hash.

Question (bonus) 1.6 une nouvelle fonction fonction Python 3.11 permet de remplacer get_sha256_hashlib(). L’identifier et si possible, la tester.

Collisions de PNG

On considère les deux versions suivantes logo v1 et logo v2 du logo de l’UCBL.

Question 1.7 comparer en binaire les deux fichiers, à quels octets diffèrent ils ? On peut utiliser l’outil cmp par exemple.

Question 1.8 calculer la somme MD5 de ces deux fichiers avec md5sum, que constatez-vous ? Pourquoi le résultat est différent avec sha256sum ?

Question 1.9 pourquoi visuellement ces fichiers apparaissent-ils comme identiques ? On donne aussi le logo original pour vous aider.

Question 1.10 expliquer pourquoi il est possible de générer de tels fichiers.

Question 1.11 donner des exemples problèmes de sécurité que cela peut poser.

Question 1.12 quelle est l’incroyable particularité de l’image suivante ?

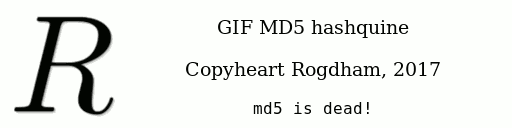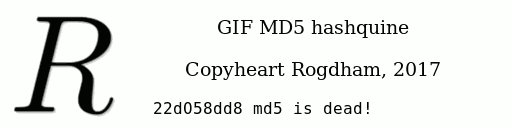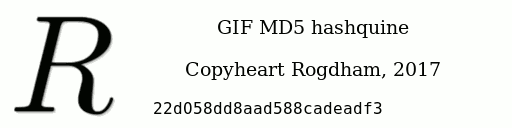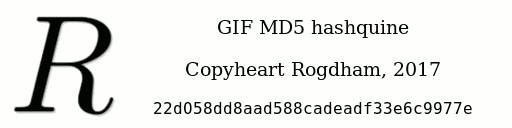
Chiffrement à clef publique RSA

Dans les TPs précédents a été implémenté le RSA naïf (textbook RSA), c’est-à-dire la version mathématique minimale définie par \(E(m) = m^{e} \pmod{n}\) et \(D(c) = c^{d} \pmod{n}\) avec les nombres \(n\), \(e\) et \(d\) choisis tels que \(D(E(m)) = (m^{e})^{d} \pmod{n} = m^{e \cdot d} \pmod{n} = m\). Cette version n’est pas sûre comme vu dans le TP2.

Contre-mesure au déterminisme de textbook RSA

Le TP2 s’est appuyé sur le déterminisme de textbook RSA pour proposer une attaque explorant un espace de recherche d’environ \(2^{24}\) messages (pour le cas où les résultats du tirage sont triés).

Question 2.1 en reprenant l’exemple de la documentation avec le schéma PKCS1_v1_5, chiffrer un message avec la clef en enregistrer le message chiffré dans un fichier binaire secret.enc.

Question 2.2 PKCS1_v1_5 pose des problèmes fondamentaux. Quel est le schéma recommandé par la documentation de PyCryptodome ? Donner le lien vers la documentation. Ici, on utilisera pas la classe TextbookRSACipher mais bien ce que PyCryptodome propose en standard.

Question (bonus) 2.3 si seuls n, e et d sont fournis, RSA.construct() calcule automatiquement p et q. Retrouver dans le code source la référence bibliographique de l’algorithme utilisé.

Une clef qui Fermat mal

On donne la clef publique RSA rsa_key_fermat.pub et un message chiffré avec cette clef challenge.enc.

Question 2.4 avec RsaCtfTool retrouver la clef secrète correspondant à rsa_key_fermat.pub.

Question 2.5 avec la clef secrète calculée par RsaCtfTool, retrouver le message secret de challenge.enc.

Question 2.6 consulter les nombres premiers \(p\) et \(q\) qui constituent la clef \(n=p \times q\), que remarque-t-on ?

Question 2.7 utiliser la factorisation par la méthode de Fermat pour retrouver \(p\) et \(q\) de rsa_key_fermat.pub. Le calcul doit être très rapide.

Si vous avez fini

Vous pouvez commencer la préparation du TP4 sur l’Oracle de parité.